
Table of Contents
Open Table of Contents
What is intelligence
Okay so let’s start with what is intelligence, The entirety of this article depends on your definition of intelligence, intelligence is not only a concept of neuroscience but also a philosophical concept and whenever you try to define stuff in philosophy things become fuzzy you can’t really get a crisp definition of intelligence, so we are going to use the following definition that works with the point of this blog well.
Intelligence is the capacity of a system to acquire, process, and apply knowledge or information in a way that enables it to adapt to its environment, solve complex problems, make informed decisions, learn from experience, and achieve goals efficiently.
Now if you do not agree with this definition of intelligence then you will pretty much disagree with most of this article.
If you haven’t been living under a rock for the last couple of years you must have at least heard about Artificial Intelligence.
(Artificial Intelligence is also a very vague term so I will be specifically talking about Artificial Neural Networks which is arguably the most powerful type of AI technique)
Let’s move on ahead and look at one of the mathematical abstractions of the human brain Artificial Neural Nets.
what are Artificial Neural Nets?
The definition says,
Artificial Neural Networks (ANNs) are a mathematical abstraction of the human brain, consisting of interconnected nodes that process information and learn to recognize patterns.
While it is technically correct but a little hard to understand I mean there is too much jargon like abstraction and nodes. let’s just see what we have to replicate on the computer.

This is a neuron, a fundamental cell in our brain that is responsible for processing and transmitting information in our brain, if we have to replicate it exactly it looks like a hard task just look at the complexity of this single cell and to then make thousands of these and make them interconnected and interact in a natural way… that sounds a little too hard and not too computationally feasible.
So we will simplify this to the extreme…

In a biological human neuron, Dendrite is how you get input/ information (as an electrical signal), the nucleus processes that input (aka input), and the processed input is sent through the axon to some other neuron for further processing.
(This is extremely simplified in actuality dendrites and axons are leaky circuits that are way more complicated to know more you can check out this Wiki article.
The initial input here can be from your senses such as vision through your optical nerve, also Keep in mind that dendrites can take input from multiple neurons at the same time)
This simple process happens millions of times in different parts of your brain and that gives rise to a glorious human being that is capable of problem-solving, critical thinking and also taking over the entire world as an apex species.
How ANNs reduce to Mathematical equations
Ok so now we want to replicate this neuron in our computers what we do is instead of electrical signals like in our brain we just use some number from 0 to 1 (0 representing no signal and 1 representing full signal)

By doing this we can represent neurons as a function, imagine the neuron above was a function named N then,
where x is the input signal and y is the output signal (y obtained after doing some operation on x).
Now let’s connect a bunch of these together.

This is how it would look, a lot of inputs and some interconnected neurons in a hidden layer and an output neuron (there could be multiple output neurons which is called an output layer).
Let’s take a close look at a single neuron and see how it functions to simulate the actual current passing through biological neuron cells.

In this diagram, there are a couple of terms that you might not be familiar with, such as Bias, weight, and Activation function
Let’s quickly explore each one of them.
- Weights: Within biological neurons, the connections extending from the dendrites to the nucleus aren’t flawless. When we transmit, for instance, 3 volts of electric current through these connections, it might not maintain that precise value by the time it reaches the nucleus. It could instead become something like 2.9999 volts or even 1.4 volts due to the varying strength of the connections. In the world of artificial neurons, this phenomenon is mirrored through the utilization of weights. These weights act as a multiplier for the input (electrical signal) to account for the differing connection strengths, replicating the variability seen in biological neurons.
- Bias: In the realm of biological neurons, communication happens through electrical signals. To transmit these signals effectively, neurons need to be charged, meaning they require an electrical potential. When a neuron receives input, its potential rises. Once it hits a specific threshold of potential, it transfers this signal to the next neuron. This threshold is known as the “action potential,” and the potential in the absence of input is termed “resting potential.” Now, in the context of artificial neurons, the bias mirrors the role of resting potential. Since resting potential isn’t zero, it’s necessary to account for it in artificial neurons. This is where the bias comes into play. It introduces a baseline level, similar to resting potential, ensuring that the artificial neuron functions effectively.
- Activation Function: Just like a biological neuron doesn’t send a signal to the next neuron until it’s ready (until it reaches action potential), an artificial neuron’s activation function acts similarly. Think of it as a gatekeeper that only allows the “electrical signal” to pass when it reaches a certain level, just like how real neurons work.
So putting it all together the function of a single neuron becomes,
In the above equation,
- = input
- = weights
- = bias (some random number)
- = an activation function, for example
- sigmoid(x) = 1 / (1 + e^-x)
- ReLU(x) = max(0, x)
NOTE: If you don’t understand any of the above, the basic point is that we can represent biological neurons as mathematical equations/functions.
If we use the Neuron function N(x1, x2,…, xn) for the entire neural network in diagram 4 then the output would be the following.
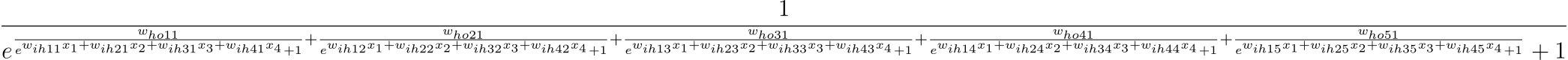
(Yes yes i know its unreadable specially on mobile devices but you get the point, its just a damn long equation, click here to get the full image)
It’s pretty massive and complicated even for such a simple neural net, but what did you think representing intelligence as a function/equation was going to be easy?
The good news is that we don’t have to calculate any of this ourselves we have computers for that and they are great at it.
The neural network we saw before (diagram 4) was just there as an example, there are other actual neural nets that do things that we might consider intelligent (according to our definition of intelligence) following are some examples.

This neural net can identify handwritten digits, which we could argue is more intelligent than a newborn human baby in this specific task.

This is a more complicated neural net with a lot more moving parts, It’s called transformer architecture can you guess what can It do?
It powers our beloved chatGPT, arguably the closest we have gotten to imitating human language and thought. GPT-3 and 4 pass the Turing test effortlessly, so this is the closest to human intelligence, or at least the closest to imitating human intelligence.
With the above examples, we can see how really complex mathematical functions can do intelligent things from detecting handwritten digits to understanding human language and using logic and mathematics (GPT)
[If you want a more practical look at Neural Nets and want to learn more about stuff we looked over such as optimization of neural nets and how to practically use them in real world, I highly recommend the Neural Networks series by 3b1b on YouTube.]
End thoughts
As we journey through the intricate corridors of understanding, we’re confronted with a revelation that shakes the very foundations of our perception. The notion that intelligence once heralded as the pinnacle of human uniqueness, might be distilled into a mathematical equation reverberates like a haunting melody across the tapestry of our minds.
In this realm of artificial neural networks, where complex computations unfold with mechanical precision, a profound question emerges: Does our cherished concept of intelligence merely echo the deterministic dance of numbers and functions? Are we, the architects of these mathematical symphonies, entrapped within the confines of our own creation?
As the veneer of mystery peels away, we’re beckoned to the crossroads of existential contemplation. The mirage of randomness dissipates, replaced by the unyielding procession of cause and effect. Each neuron’s pulse, every synaptic connection, becomes an echo of inevitability, orchestrating the grand narrative of existence with unfaltering certainty.
Yet, even in the face of such deterministic revelation, a subtle spark of wonder remains. Perhaps, it’s the very acknowledgment of our place within this intricate web of mathematics that opens the gateway to profound questioning. Are we the products of algorithms, or do we possess the power to transcend the boundaries of our creation?
In the boundless expanse of the universe, as we gaze upward and inward, a symphony of questions unfolds. Does the unraveling of intelligence’s enigma lead us toward a deeper understanding of our own essence? Do we find meaning in acknowledging that the universe, too, adheres to a cosmic code?
In the echoing silence of this revelation, we are left with a fleeting glimpse of the eternal question: What lies beyond the equations? Is there a realm where the heart and the spirit transcend the bounds of determinism, embracing the enigma of existence in all its raw, unquantifiable glory?
The journey continues, and as we explore the echoes of intelligence and the universe, let us pause to embrace the ambiguity, to dwell in the awe, and to revel in the boundless expanse of the unknown.